Diffie-Hellman Açar Mübadiləsi
Tutaq ki, siz bəzi məlumatları AES kimi alqoritm ilə şifrələyib dostunuza göndərmək istəyirsiniz. Şifrələnmiş mətni deşifrə etmək üçün dostunuzun sizin gizli açarınızı bilməsi vacibdir. Bu məsələ “key distribution problem” adlanır və xoşbəxtlikdən iki əsas həll yolu vardır:
- Həll 1: Dostunuzla görüşürsünüz və açarı ona təqdim edirsiniz (uzaq məsafə üçün yaramır).
- Həll 2: Riyaziyyatdan istifadə edərək DHKE protokolunu tətbiq edirsiniz.
Bu gün biz daha praktik və təhlükəsiz olan Diffie-Hellman açar mübadiləsi (dəyişməsi) protokolu haqqında danışacağıq.
DH Açar Mübadiləsinin İşləmə Prinsipi
Diffie-Hellman açar mübadiləsi iki tərəfin gizli açarı ictimaiyyətə açıqlamadan müəyyən etməsinə imkan verən riyazi modeldir. Konsepsiya modul arifmetikasından və böyük sadə ədədlərdən istifadə edir ki, bu da “bruteforce” hücumlarını vaxt-alıcı edir. Diffie-Hellman 1976-cı ildə icad edilmişdir və o vaxtdan bəri bir çox sistemlərdə istifadə edilir.
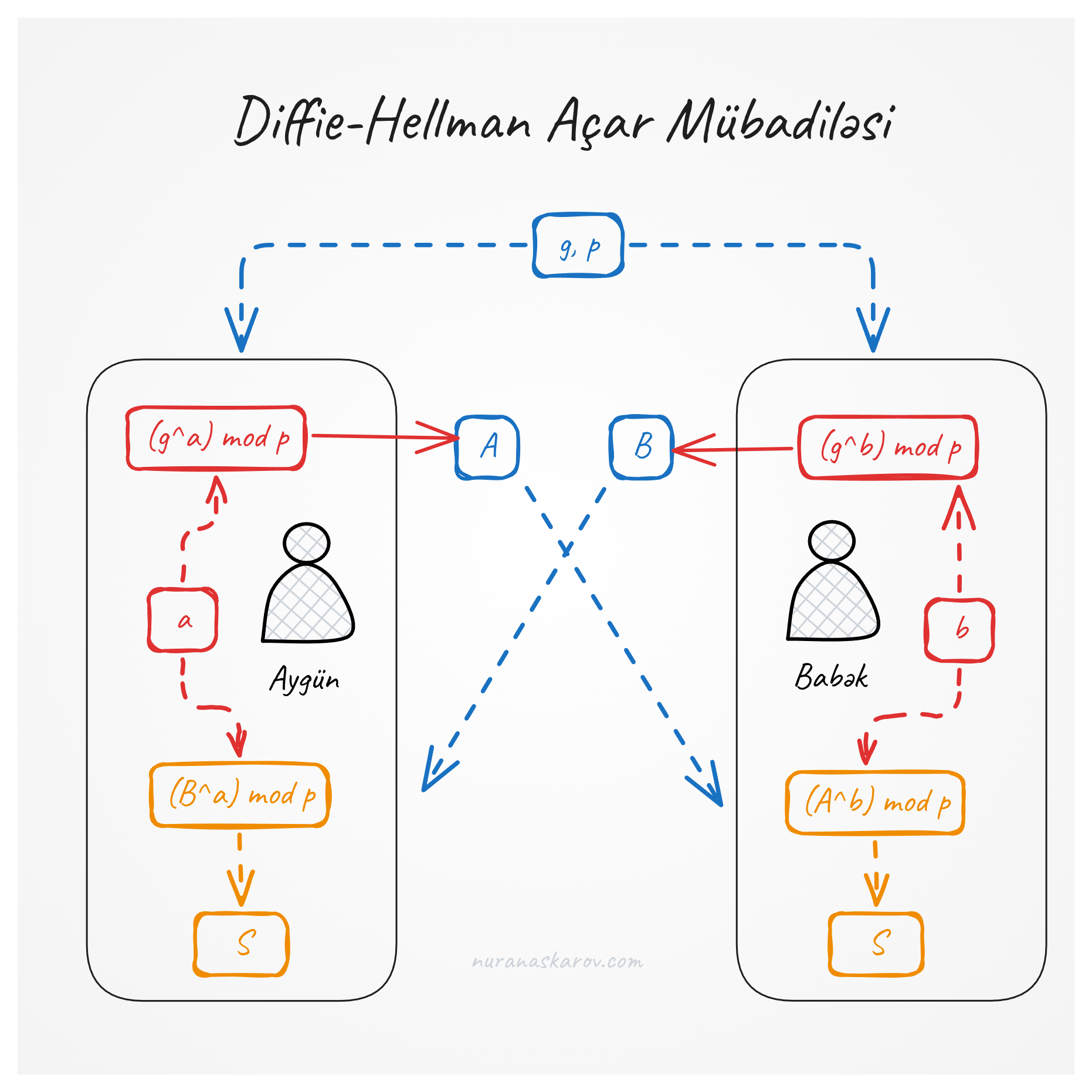
Addım 0: İctimai Sabitlər
Əvvəlcə hər kəsin görə biləcəyi iki ictimai sabitə razılaşmaq lazımdır:
- g - çox kiçik bir ədəd, “generator” adlanır, adətən 2 və ya 5.
- p - nəhəng sadə ədəd, “prime” adlanır, çox vaxt 2048+ bit uzunluğundadır.
Bu dəyərlər o qədər ümumidir ki, TLS, SSH və VPN kimi sistemlər hər dəfə sadə ədədlər yaratmaq əvəzinə standartlaşdırılmış rəqəmlərdən istifadə edir.
Məsələn, bir çox alətlər RFC 3526 standart spesifikasiyasında göstərildiyi kimi aşağıdakı dəyərlərdən istifadə edir:
g = 2
p = FFFFFFFF FFFFFFFF C90FDAA2 2168C234 C4C6628B 80DC1CD1
29024E08 8A67CC74 020BBEA6 3B139B22 514A0879 8E3404DD
EF9519B3 CD3A431B 302B0A6D F25F1437 4FE1356D 6D51C245
E485B576 625E7EC6 F44C42E9 A637ED6B 0BFF5CB6 F406B7ED
EE386BFB 5A899FA5 AE9F2411 7C4B1FE6 49286651 ECE45B3D
C2007CB8 A163BF05 98DA4836 1C55D39A 69163FA8 FD24CF5F
83655D23 DCA3AD96 1C62F356 208552BB 9ED52907 7096966D
670C354E 4ABC9804 F1746C08 CA237327 FFFFFFFF FFFFFFFF
Addım 1: Mən Öz Gizli Açarımı Yaradıram
Mən təsadüfi bir “a” ədədi seçirəm və öz xüsusi açarımı hesablayıram:
A = (g^a) mod p
Burada bəzi məqamlar var.
| Əməliyyat | İzah | Misal |
|---|---|---|
| x ^ y | Qüvvətə yüksəltmə | 2^3 = 2x2x2; 5^2 = 5x5. |
| x mod y | Mod funksiyası (Evklid bölməsinin qalığı) | 5 mod 2 = 1; 6 mod 3 = 0; 6 mod 2 = 0. |
“mod” böyük ədədi məhdud diapazonda yerləşdirməyə kömək edir və bu xüsusiyyətinə görə kriptoqrafiyada geniş istifadə olunur.
Addım 2: Dostum da Eynisini Edir
Dostum öz təsadüfi “b” ədədini seçir və öz xüsusi açarını hesablayır:
B = (g^b) mod p
Addım 3: Açarları Mübadilə Edib Gizli Açarı Hesablayırıq
İndi biz ictimai dəyərlərimizi mübadilə edirik:
- Mən A-nı dostuma göndərirəm.
- Dostum B-ni mənə göndərir.
- İndi hər ikimiz S-i müstəqil şəkildə hesablaya bilərik.
# Mənim hesablamam
S = (B^a) mod p
# Dostumun hesablaması
S = (A^b) mod p
Hər iki hesablamada eyni nəticəni əldə edirik və, ən əsası, bunu açıq şəkildə heç kimlə paylaşmırıq.
İndi mən “S” açarını istifadə edərək məlumatları AES-256 ilə şifrələyə bilərəm, dostum isə bunu deşifrə etməkdə heç bir problem yaşamayacaq.
Əgər kimsə qırağdan içtimai “n”, “g”, “A”, “B” kimi parametrləri görərək “S”-i hesablamaq üçün alqoritmi sındırmağa cəhd etsə, bu proses o qədər çox vaxt və resurs tələb edəcək ki, adətən belə bir cəhd praktiki hesab edilmir.
Təhlükəsizlik Məsələləri
DHKE-nin ən əhəmiyyətli zəif cəhəti “Ortada Adam” (man-in-the-middle) hücumlarına qarşı acizdir, burada hücumçu tərəflər aradakı kommunikasiyanı kəsə və dəyişə bilər.
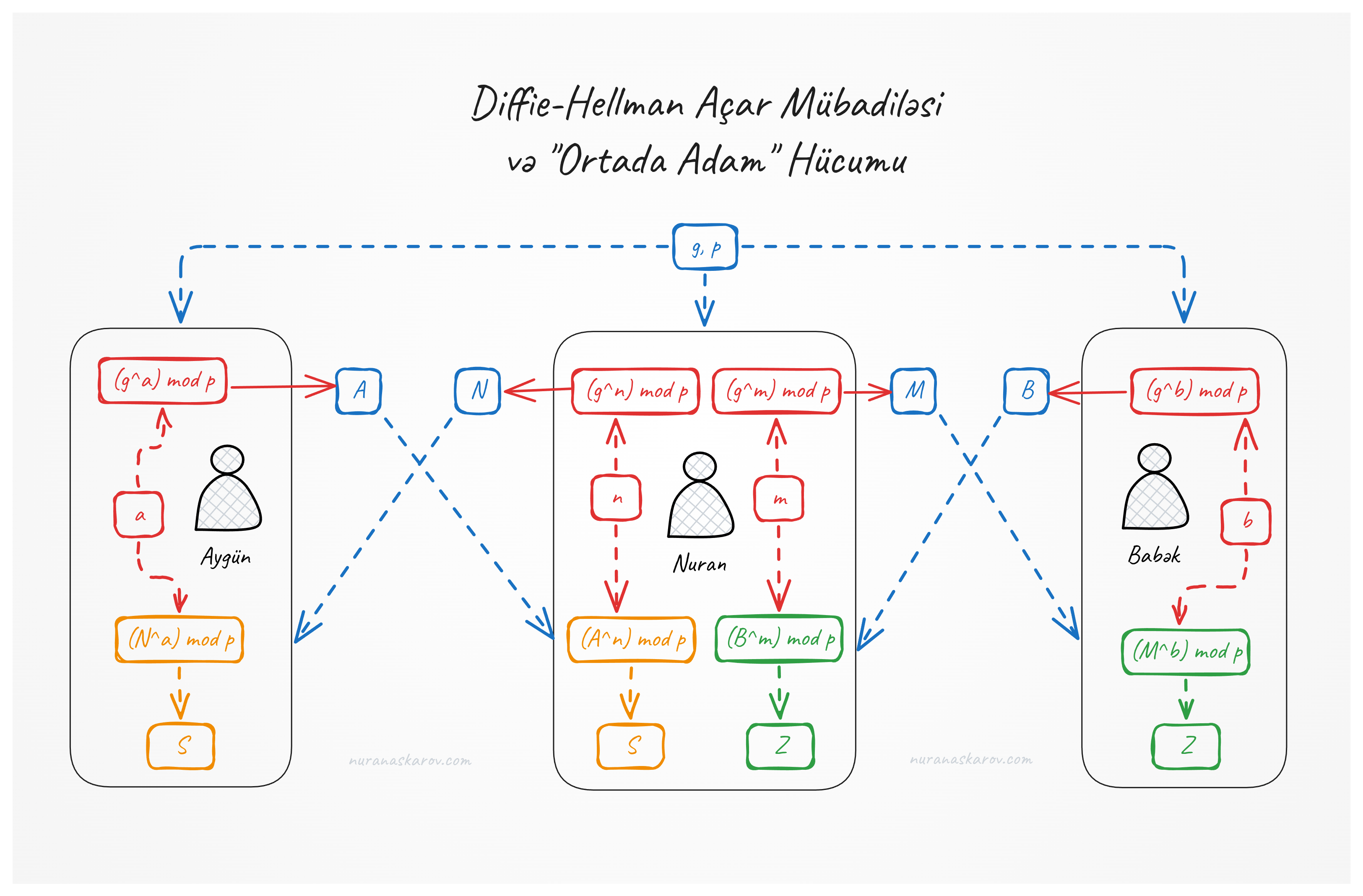
Açar seçimi üçün zəif təsadüfi ədəd generasiyası və ya kifayət qədər böyük olmayan sadə ədədlər diskret loqarifm problemini həll etməyi asanlaşdıra bilər.
Kvant hesablamalarına gəldikdə isə, Şorun alqoritmi ənənəvi DHKE-ni klassik kompüterlərdən eksponensial dərəcədə sürətli həll edərək poza bilər.
Elliptik Əyri Variantı
Alternativ olaraq, ECDHKE kimi tanınan elliptik əyri variantı mövcuddur. Bu metod klassik DHKE ilə eyni səviyyədə təhlükəsizlik təklif edir, lakin daha kiçik açar ölçüləri istifadə edir. Riyaziyyat modul eksponentiasiya əvəzinə sonlu sahədə elliptik əyri nöqtələri üzərində əməliyyatlar aparmağı əhatə edir. Effektivliyinə görə daha çox istifadə olunur.
Bu məqaləni oxuduğunuz üçün təşəkkür edirəm. Diffie-Hellman açar mübadiləsini ilk dəfə öyrəndiyim zaman bu riyazi texnikanın zərifliyi məni çox heyran etdi.